• Wstęp
• Wzory interakcyjne według EC1993-1-1
  • Zginanie ze ścinaniem
  • Zginanie z siłą podłużną
  • Zginanie ze ścinaniem i siłą podłużną
• Interakcja wg EC1993-1-8
• Interakcja dla stali wg EC1992-4
• Wzory interakcyjne dla prętów gwintowanych i zbrojeniowych
  • Wzory interakcyjne
• Porównanie wykresów interakcyjnych
• Wyznaczanie maksymalnego momentu zginającego

Wstęp

Na wstępie chciałbym zaznaczyć, że post ten dotyczy stali gwintowanej i zbrojeniowej wykorzystywanej w połączeniach prefabrykatów. Choć oczywiście część przedstawionych tu wzorów i założeń można stosować w odniesieniu do stali używanej i w innych sytuacjach.

Jednym z przyjętych założeń jest to, że pręty mogą być poddane działaniu trzech rodzajów sił. Podłużnej N (rozciągającej lub ściskającej), ścinającej V i momentu zginającego M. Wzory do obliczania przedstawiłem w poprzednim poście. Jeśli na przekrój działa więcej niż jeden rodzaj sił, to należy w obliczeniach zastosować odpowiednią redukcję nośności. Stan, w którym pręt osiąga swoją nośność w zależności od naprężeń które na niego działają, nazywamy kryterium zniszczenia. Dla elementu stalowego kryterium to możemy wyznaczyć np. z pomocą kryterium von Misesa-Hencky’ego.

Przy obliczaniu nośności przekroju możemy też skorzystać ze wzorów i warunków podanych w  Eurokodzie EC1993-1-1[1]. Norma ta umożliwia także wyznaczenie nośności elementu z uwzględnieniem jego stateczności. Jest to ważny punkt obliczeń prętów ściskanych, gdyż o utracie nośności decydować tu mogą efekty drugiego rzędu.

Wzory interakcyjne według EC1993-1-1

W podstawowej normie do obliczania elementów stalowych EC1993-1-1[1] znajdziemy wzory na  obliczenie nośności przekroju na rozciąganie, ścinanie i zginanie. Podane są tu również wzory i założenia umożliwiające uwzględnienie równoczesność działania tych sił. Poniżej zebrałem te informacje, które mogą być przydatne przy obliczaniu naszych elementów.

Zginanie ze ścinaniem:

Zgodnie z punktem 6.2.8(2) wpływ ścinania na nośność przy zginaniu nie musimy uwzględnić,  gdy siła poprzeczna nie przekracza 50% nośności plastycznej przekroju przy ścinaniu. W przeciwnym wypadku musimy zastosować zredukowaną granicę plastyczności.

Wykres obwiedni nośności na zginanie (m) z uwzględnieniem nośności na ścinanie (v) można przedstawić  za pomocą wykresu:

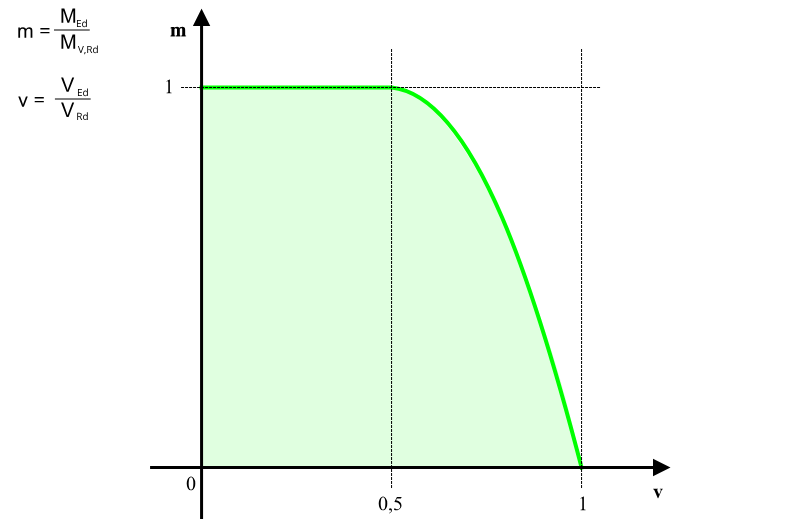
Zginanie z siłą podłużną:

Zgodnie z normą [1] musi być spełniony warunek:

Wykres zależności nośności na zginanie od nośności na rozciąganie przyjmuje postać:

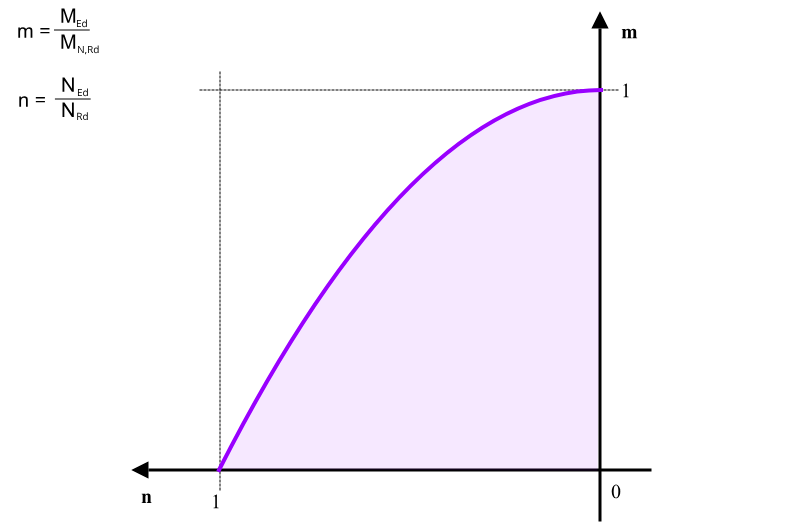
Zginanie ze ścinaniem i siłą podłużną:

Zgodnie z punktem 6.2.10(2) wpływ ścinania na nośność przy zginaniu nie musimy uwzględnić,  gdy siła poprzeczna nie przekracza 50% nośności plastycznej przekroju przy ścinaniu. W przeciwnym wypadku musimy zastosować zredukowaną granicę plastyczności.

Zredukowaną nośność na zginanie przekroju można przedstawić wzorem:

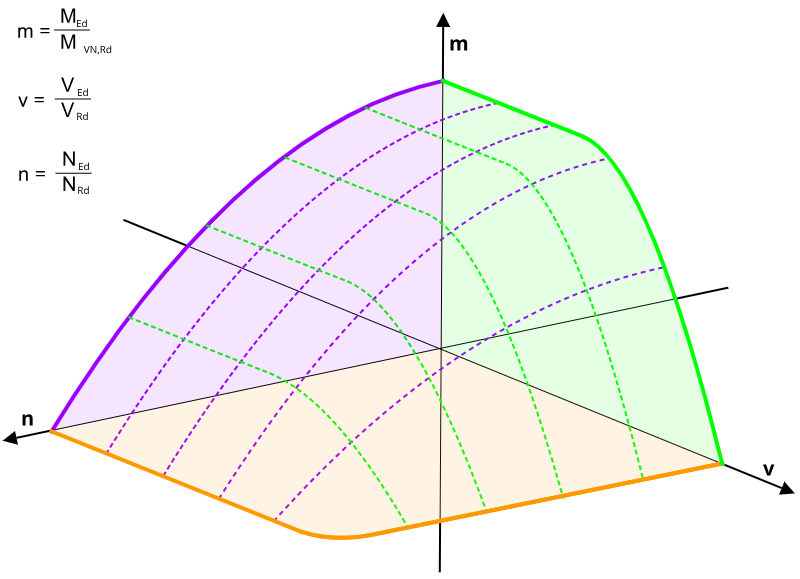
Interakcja wg EC1993-1-8

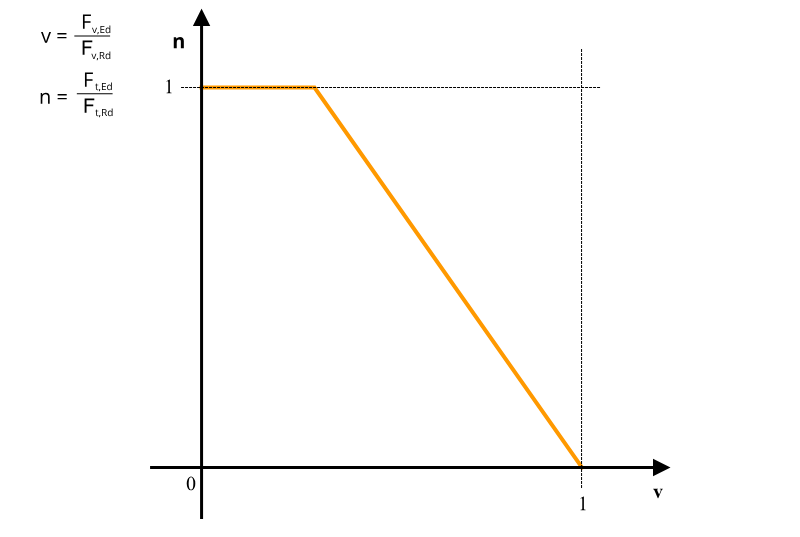
Z normy EC1993-1-8 [2] możemy skorzystać przy obliczaniu prętów gwintowanych. W Tablicy 3.4 znajduje się wzór pozwalający uwzględnić jednoczesne działanie siły rozciągającej i ścinającej.

Interpretacją powyższej zależności jest wykres:

Interakcja dla stali wg EC1992-4

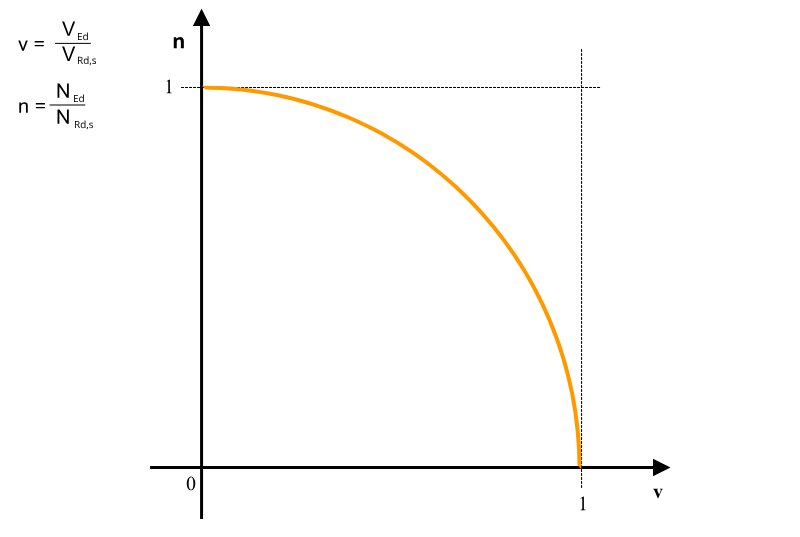
Norma EC1992-4 [3] dotyczy projektowania zamocowań w betonie. Według jej zapisów dla elementów stalowych należy sprawdzić warunek:

Wzory interakcyjne dla prętów gwintowanych i zbrojeniowych

Rozpatrując stalowe pręty wspornikowe gwintowane czy zbrojeniowe, sprawdzenia interakcji sił można dokonać zgodnie z normą EN1993-1-1 tak jak powyżej, albo np. posłużyć się wzorami opartymi na kryterium zniszczenia. Tak jak wspomniano na wstępie, zakłada się, że elementy mogą one być obciążone siłą normalną, ścinającą i zginającą. Tu uwaga, wzory interakcyjne przedstawione w dalszej części poniżej nie mogą być stosowane do przypadków ogólnych obliczania konstrukcji stalowych. Są one opracowane dla krępych  przekrojów (pełne okrągłe) elementów wspornikowych.
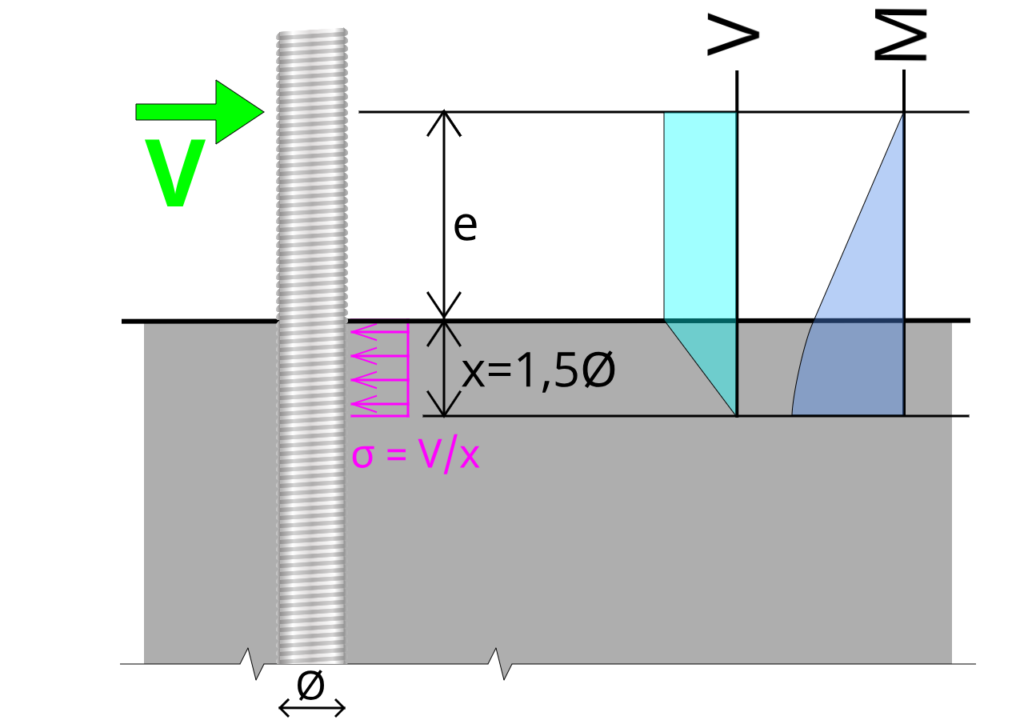
Przy obliczaniu nośności prętów w połączeniach będę przyjmował, że maksymalne siły występują w tym samym przekroju pręta. Jednakże w rzeczywistości maksymalny moment i maksymalna siła ścinająca występują na innej długości elementu.

Wzory interakcyjne

W dalszej części będę stosował oznaczenia:

Wzory interakcyjne stosujemy w zależności od warunków w jakich pracuje dany pręt. Rozróżniamy trzy podstawowe warianty:

– pręt długi: o długości większej od 2Ø

– pręt krótki: o długości mniejszej lub równej 2Ø

– pręt przyspawany do płytki stalowej z pełnym kontaktem między płytką, a powierzchnią betonu (e=0)

1. Jeśli pręt ma długość wspornika > 2Ø to należy sprawdzić warunek:

2. Jeśli mamy pręt krótki e  ≤  2Ø to należy dodatkowo poza powyższym sprawdzić warunek uwzględniający ścinanie:

Jeśli jednak płytkę stalową łączymy z prętem za pomocą śruby, to sprawdzenia dokonujemy jak dla pręta krótkiego.

Zasady te zebrałem na rysunku poniżej.

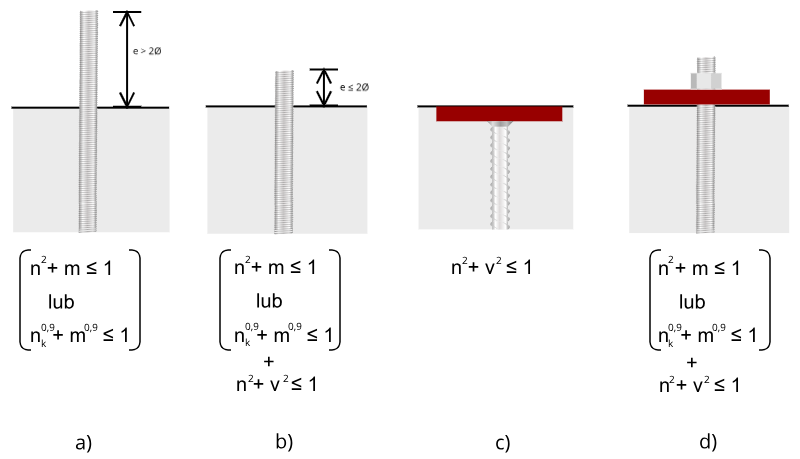
Powyższe wzory zostały opracowane wg kryterium zniszczenia i można je też opisać jako:

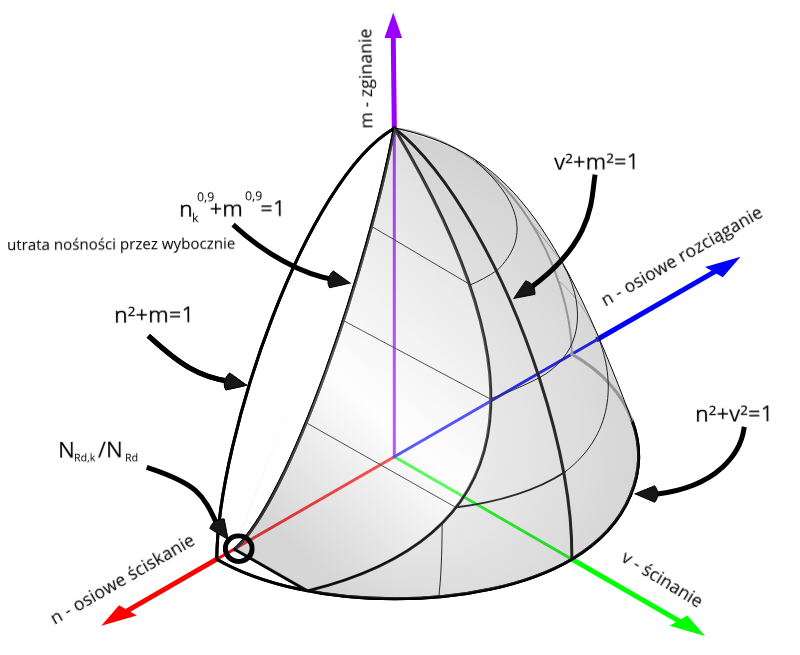
Porównanie wykresów interakcyjnych

W tym miejscu chciałbym jeszcze porównać wykresy wyznaczone wg poszczególnych norm i metod.

Zginanie ze ścinaniem:

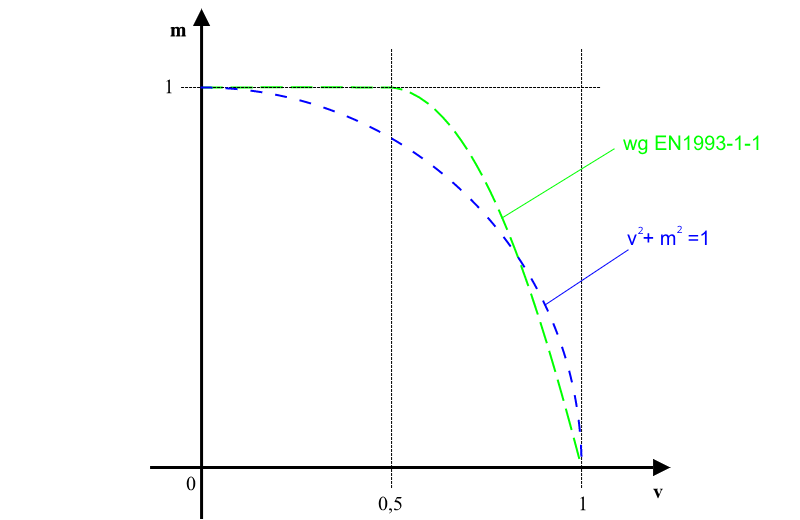
Zginanie z siłą podłużną:

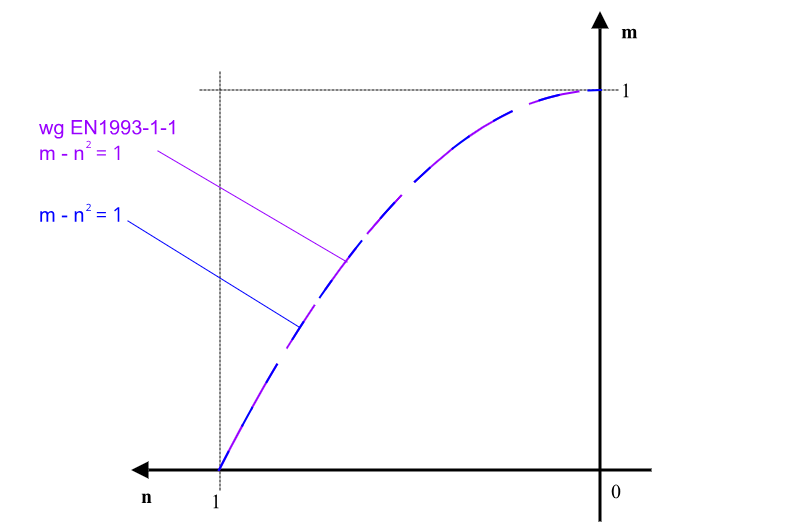
Siła normalna i ścinająca:

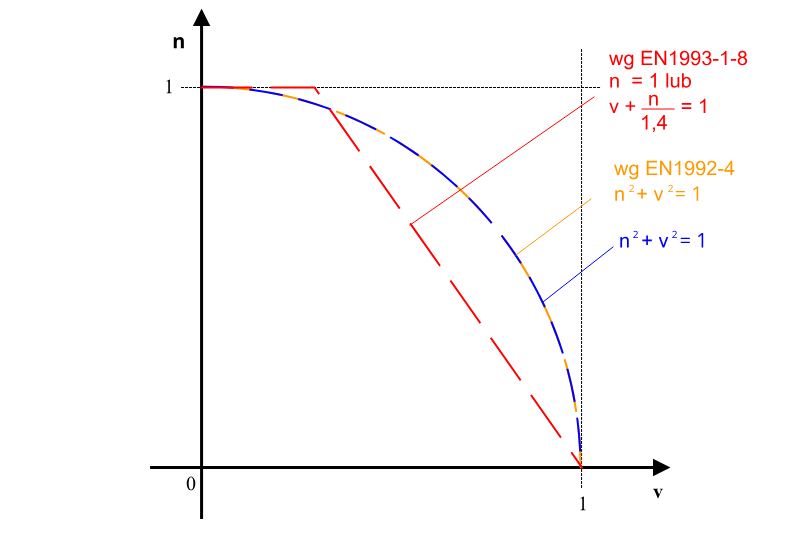
Wyznaczanie maksymalnego momentu zginającego

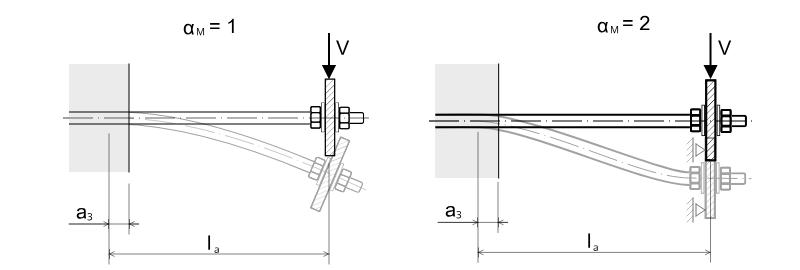
Korzystając ze schematu przedstawionego na rysunku 1 możemy wyznaczyć maksymalny moment zginający w pręcie utwierdzonym w betonie.

Bibliografia:

[1] PN-EN1993-1-1 Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
[2] PN-EN1993-1-8 Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
[3] EN1992-4 Eurokod2 – Projektowanie konstrukcji z betonu – Część 4: Projektowanie zamocowań do stosowania w betonie
[4] Betongelementboken Bind B. Avstivning og kraftoverføring. 2016.